今天主要來聊聊分子的振動模式。首先,我們來介紹一下分子的振動自由度。分子的運動由平動、轉(zhuǎn)動和振動三部分組成。假設(shè)一個分子中的原子數(shù)為N,則該分子總共具有3N個運動自由度,其中需要3個空間坐標(biāo)來確定分子質(zhì)心的位置,3個坐標(biāo)來確定分子在空間的取向(如果是直線分子,則只需要2個坐標(biāo)即可),由此我們可以得出對于非直線分子,振動自由度為3N-6;而對于直線分子,振動自由度為3N-5。讓我們以氧氣分子為例,由于是雙原子分子,故只有一個振動自由度。顯然該振動是中心對稱的。非對稱振動對應(yīng)紅外吸收,而對稱振動對應(yīng)拉曼散射。對于氧氣分子,由于沒有任何偶極矩的變化,自然可以對應(yīng)上面的結(jié)論,作為一個中心對稱的分子,是沒有紅外吸收光譜的。讓我們再來看另外一個例子,一氧化氮(NO),由于既有極性變化,也有偶極矩變化,因此它同時具有拉曼光譜以及紅外光譜。
以上說到的都是雙原子分子,現(xiàn)在,我們來看一些三原子分子。根據(jù)對振動自由度的計算方式,三原子分子具有3個振動模式:對稱伸縮振動、彎曲/變形振動、不對稱伸縮振動。具體表現(xiàn)形式如下所示:
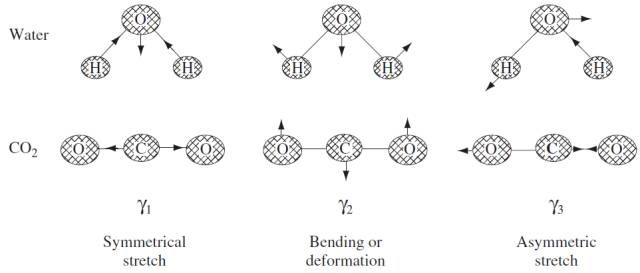
上圖展示了H2O和CO2分子的三種振動模式,采用了小球彈簧模型,不知道大家還是否記得中學(xué)時候?qū)W過的胡克定律,小球即原子,彈簧即化學(xué)鍵。彈簧越緊,小球質(zhì)量越輕,振動頻率就越高。
該模型被廣泛用于解釋振動光譜,然而,對于分子而言,除了化學(xué)鍵和原子以外,電子濃度也是一個變量。隨著分子的振動,電子云的變化會引起分子偶極矩或者極性的變化。對于三原子分子而言,對稱伸縮振動將引起極性變化從而帶來強(qiáng)拉曼散射,而變形振動則會引起偶極矩變化,從而導(dǎo)致強(qiáng)紅外吸收。
以上分析均只針對于小分子,對于復(fù)雜的大分子而言,對其振動的分析將更加困難。我們需要將每個小分子的振動光譜都計算出來,而由于大分子本身的復(fù)雜性,目前要完成這樣的計算幾乎不可能。現(xiàn)在的做法是將一個振動分子的混亂內(nèi)部結(jié)構(gòu)看作是由許多相當(dāng)簡單的振動組合而成的,應(yīng)用群論來對分子的振動模式進(jìn)行分析。
文章來源:拉曼光譜公眾號
文章鏈接:分子的振動模式
文字報道:袁偉
文章編輯:董榮錄